Kunstis või kirjanduses võib-olla on ilu viimastel aastatel kaotanud oma valuuta kui hindamisstandard või tipptaseme kriteerium, mida peetakse liiga subjektiivseks või kultuuriliselt vahendatuks. Matemaatikute jaoks pole ilu kui igavene tõde aga kunagi moest välja läinud. “Ilu on esimene katse: koledal matemaatikal pole siin maailmas püsivat kohta, ” kirjutas Briti numbriteoreetik Godfrey Hardy 1941. aastal.

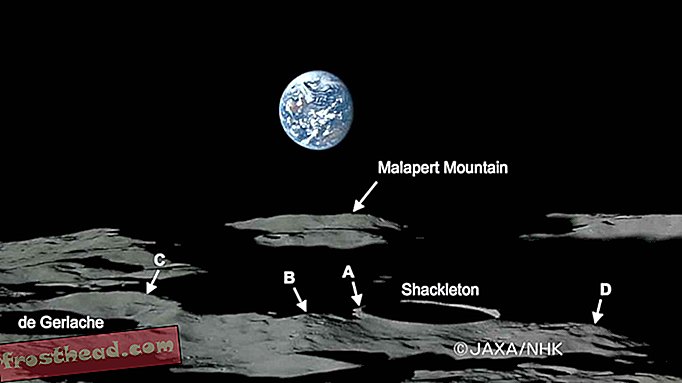
Matemaatilise ilu maitsmiseks liikuge kõigepealt oma lemmik pubisse ja tellige härmas kruus õlut. Asetage see kolm korda paberist vaibale, moodustades kolm kondenseerumisrõngast - veenduge, et see toimub nii, et kõik kolm rõngast lõikuvad ühel hetkel. Nüüd küsige oma kaaslastelt: kui suurt kruusi oleks vaja ülejäänud kolme ristumispunkti katmiseks? Peaaegu alati eeldatakse, et ainult hiiglaslik kruus teeniks seda eesmärki. Üllatusvastus: sama kruus! See on täiesti lollikindel lahendus. (Vt vasakul olevat joonist, kus on näha kaks võrdselt kehtivat lahendust; mõlemal juhul on tahked ringid kolm esimest rõngast; katkendlik ring on neljas ring, mis tähistab ülejäänud kolme ristumispunkti katvat kruusi.)
Selle teesi avaldas Roger A. Johnson 1916. aastal. Johnsoni ringi teoreem näitab kahte matemaatilise ilu olulist nõuet. Esiteks on see üllatav. Te ei eelda, et sama suurusega ring kuvatakse uuesti lahenduses. Teiseks on see lihtne. Kaasatud matemaatilised mõisted, ringid ja raadiused, on põhiprobleemid, mis on ajaproovile vastu pidanud. Johnsoni teoreem tuleb aga iluteenuste osakonnas ühes silmatorkavas osas lühidalt välja. Parimad teoreemid on ka sügavad, sisaldavad paljusid tähenduskihte ja paljastavad rohkem, kui nende kohta rohkem teada saate.
Millised matemaatilised faktid vastavad sellele kõrgele ilutasemele? Saksa matemaatik Stefan Friedl on toetanud Grigory Perelmani geometriseerimisteoreemi, mille tõestus esitati alles 2003. aastal. Teoreem, mis tekitas matemaatikute maailmas sensatsiooni, edendab kolmemõõtmelise topoloogilise klassifikatsiooni võtmeetappi. tühikud. (Võite mõelda nendele ruumidele kui võimalikele alternatiivsetele universumitele.) "Geometriseerimise teoreem, " väidab Friedl, "on hämmastava ilu objekt."
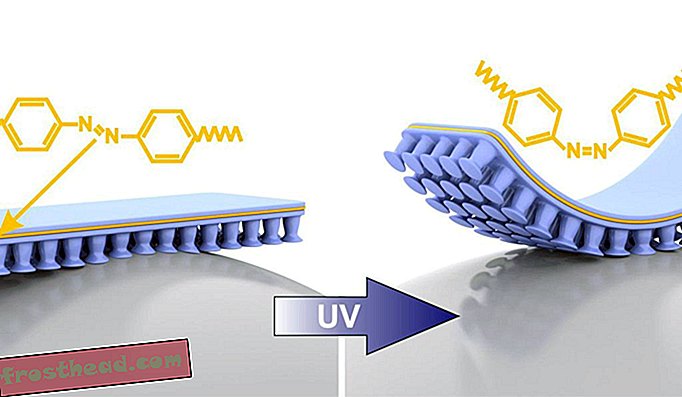
Keerutatuna kõige lihtsamateks terminiteks on see, et enamikul universumitest on looduslik geomeetriline struktuur erinev sellest, mida me keskkoolis õpime. Need vahelduvad universumid ei ole eukleidilised ega lamedad. Küsimus on seotud ruumi enda kumerusega. Selle tähenduse seletamiseks on mitmeid viise; matemaatiliselt on kõige täpsem öelda, et vahelduvad universumid on pigem hüperboolsed või negatiivselt kaardunud, mitte lamedad.
Matemaatikud alles hakkavad tagajärgedega hakkama saama. Astrofüüsikalised andmed näitavad, et meie enda universum on tasane. Kuid nendes vahelduvates universumites pole tasasus loomulik olek. Perelmani teoreemi kohaselt on meie näiliselt tasane universum üllatav erand.
Veel üks põhjus, miks teoreem rahvusvahelise publiku tähelepanu köitis, on seotud matemaatiku endaga. Aastal 2010 kahandas veetlev venelane miljoni dollari auhinna läbimurde eest Massachusettsi Cambridge'i savi matemaatika instituudist. Ilmselt polnud Perelmani jaoks matemaatiline ilu asi, mida sai osta ja mille eest maksta. Meie arusaama muutmine universumist oli piisavalt tasu.